컴퓨터에 지구를 위치시키는 법 (feat. Geographic Coordinates)

컴퓨터로 지구 또는 지구안에 있는 무언가를 표현하려면 경도, 위도같은 좌표가 필요하다.

• Cartesian Coordinates (데카르트 좌표계)
• Geographic Coordinates (지리적 좌표계)

---

 

Geographic Coordinates (지리적 좌표계)

• Cesium에서는 Cartographic 객체
• spherical coordinate: (azimuth, inclination, radius) 로 표현 - (방위각, 경사도, 반경)
• geographic coordinates : (longitude, latitude, height) 로 표현 - (경도, 위도, 높이)
  • 경도: 서쪽에서 동쪽으로의 각도 (기준선 = 본초 자오선)
    • 본초 자오선 = 0º
    • 서쪽 = -180º
    • 동쪽 = +180º
  • 위도: 남쪽에서 북쪽으로의 각도 (기준선 = 적도)
    • 적도 = 0º
    • 남반구 = -90º
    • 북반구 = +90º
  • 높이: 표면 위 또는 아래로의 선형거리
• 대부분의 벡터 데이터는 Geographic 으로 표현
  • GPS 등에 Geographic 이용

---

 
경위도 $(0^◦, 80^◦)$에서 $(10^◦, 90^◦)$의 면적과 $(0^◦, 0^◦)$에서 $(10^◦, 10^◦)$을 비교해보자. 얼핏보면 각도의 제곱이 같기 때문에 면적이 같을 것 같다.

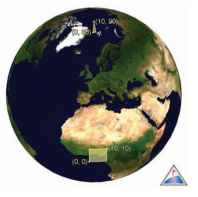
하지만 지구는 3차원 타원체다. 즉, 위치에 따라 편평률이 다르기 때문에 경위도 $(0^◦, 80^◦)$에서 $(10^◦, 90^◦)$ 면적과 $(0^◦, 0^◦)$에서 $(10^◦, 10^◦)$ 면적은 서로 다르다.
 
따라서 지리적 그리드 테셀레이션에서와 같이 극 근처의 균일한 경도/위도 그리드 오버샘플을 기반으로 하는 알고리즘이 필요하다. (나중에 설명)
 

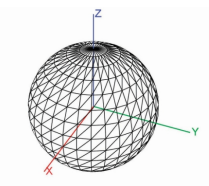
사람들은 경, 위도에 익숙하다. 예를 들어, 대한민국 경위도는 127º, 37.5º 이다.
하지만 지구의 중심을 기준으로 대한민국의 데카르트 좌표는 다음과 같다.

 

X ≈ −3,044,804 m,
Y ≈ 4,043,821 m,
Z ≈ 3,884,000 m
 
사람들은 이런 표현에 익숙하지 않다. 하지만 컴퓨터는 이런 방식을 통해 무언가를 나타낸다.
대한민국 경위도를 데카르트좌표로 변환하는 방법을 알아보자.

---

 

원점을 중심으로 구의 방정식: $x_s^2 + y_s^2 + z_s^2 = r^2$ (2.1)

 
1. 방정식 (2.1)을 만족하는 점($x_s, y_s, z_s)$는 구의 표면(surface)에 있다.
2. 구(sphere)에 있는 점의 경우, 점을 원점을 기준으로 벡터로 취급하고 정규화 하면 표면 법선을 구할 수 있다.
 
지구를 구로 표현하면 계산이 용이하겠지만, 지구는 타원체이기에 타원체 방정식을 사용하는 것이 더 정밀하고 유연하다.
 

타원체 방정식: $\frac{x_s^2}{a^2} + \frac{y_s^2}{b^2} + \frac{z_s^2}{c^2} = 1$ (2.2)

 
1. 타원체는 각각 X축, Y축, Z축을 따라 세개의 반지름(a, b, c)로 정의된다.
2. 방정식 (2.2)를 만족하는 점($x_s, y_s, z_s)$는 타원체의 표면(surface)에 있다.
 

타원체의 한 점에서 지구 중심을 기준으로 법선을 그리면 이를 Geocentric이라고 한다.
하지만 타원체는 곡률이 존재하기 때문에, Geocentric은 대부분 점에 대해 표면에 수직이 아니다.
 
따라서 타원체의 한 점에서 지구 중심이 아닌 적도$(X, Y)$ 평면에 법선을 그려야 한다. 이를 Geodetic이라고한다.
Geodetic은 타원에 한 점에 대해 실제 법선이다.
 
구의 경우, Geodetic, Geocentric은 동일하다.
타원체는 대부분 점에 대해 Geodetic, Geocentric이 크게 다른데, 45º에서 가장 크게 다르다.

 
표면 법선 벡터(surface normal vector) = $\hat{n_s}$ 구하기

$m = (\frac{x_s}{a^2}, \frac{y_s}{b^2}, \frac{z_s}{c^2})$
$\hat{n_s} = \frac{m}{||m||}$

 

Geocentric 오차

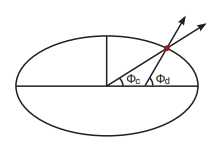
지구 중심에서 특정 벡터 사이의 각도 : $\phi_c$ = geocentric

지구 표면에서 특정 벡터 사이의 각도 : $\phi_d$ = geodetic

위경도를 geocentric 또는 geodetic으로 구한 후, 높이(h)는 geodetic을 이용해서 구해야 한다.
 
높이(h)를 geocentric으로 구할 경우 우주와 같이 높이가 높은 곳에서 오차가 발생한다.
특히 geocentric, geodetic 각도 차이가 클 수록 오차가 커진다.

---

 

좌표 변환

Geographic coordinates → WGS84

실제 지리 데이터가 저장될 때는, 보통 경위도(지리적 좌표)로 저장된다.
 
컴퓨터에서 지구는 보통 WGS84 좌표계로 렌더링하기 때문에 경위도를 WGS84 좌표로 변환하는 작업은 필수적이다.
 
주의: WGS84 또한 Geographic coordinates 중 하나다.

• 전 세계에서 가장 널리 사용되는 지리 좌표계 (GPS 표준)
• 즉, WGS84는 Geographic Coordinates 중 하나일 뿐
• GCS(Geographic Coordinate System) ≠ WGS84
• WGS84 ⊂ GCS
• 원점: 지구 중심(Geocentric)
• 단위: 도(º)
• 좌표값: (위도, 경도, 타원체 고도)

---

 

 

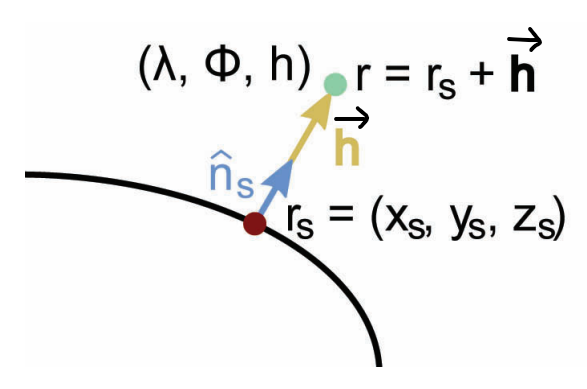
$\hat{n_s} = \cos\phi \cos\lambda\hat{i} + \cos\phi \sin\lambda\hat{j} + \sin\phi\hat{k}$ (2.3)

구(Sphere)형 모델에서 유도된 형태이며, 완전한 타원체 모델을 표현하기 위해 추가 변환이 필요하다.
 

$\overrightarrow{n_s} = \frac{x_s}{a^2}\hat{i} + \frac{y_s}{b^2}\hat{j} + \frac{z_s}{c^2}\hat{k}$ (2.4)

타원체 표면에서의 법선 벡터를 나타내는 식  (단위벡터 아님)
 

$\hat{n_s} = \gamma \overrightarrow{n_s}$ (2.5)

임의의 $\gamma$를 곱해 단위벡터를 찾을 수 있다.
 

$\hat{n_s} = \gamma(\frac{x_s}{a^2}\hat{i} + \frac{y_s}{b^2}\hat{j} + \frac{z_s}{c^2}\hat{k})$ (2.6)

(2.4)의 법선 벡터를 (2.5)의 관계를 통해 단위 벡터로 변환하는 식
 

$\hat{n_x} = \frac{\gamma x_s}{a^2}$
$\hat{n_y} = \frac{\gamma y_s}{b^2}$ (2.7)
$\hat{n_z} = \frac{\gamma z_s}{c^2}$

단위 법선 벡터의 성분을 타원체 좌표 $(x_s, y_s, z_s)$와 타원체 반지름 $(a, b,c)$로 나타낸 식
 

$x_s = \frac{a^2\hat{n_x}}{\gamma}$
$y_s = \frac{b^2\hat{n_y}}{\gamma}$ (2.8)
$z_s = \frac{c^2\hat{n_z}}{\gamma}$

단위 법선 벡터 성분을 이용하여 타원체 표면의 좌표 $(x_s,y_s,z_s)$로 나타낸 식
 

타원체 방정식 $\frac{x_s^2}{a^2} + \frac{y_s^2}{b^2} + \frac{z_s^2}{c^2} = 1$에 $(x_s,y_s,z_s)$ 대입

$\frac{(\frac{a^2 \hat{n_x}}{\gamma})^2}{a^2} + \frac{(\frac{b^2 \hat{n_y}}{\gamma})^2}{b^2} + \frac{(\frac{c^2 \hat{n_z}}{\gamma})^2}{c^2} = 1$

 
정리하면

$a^2\hat{n_x}^2 + b^2\hat{n_y}^2 + c^2\hat{n_z}^2 = \gamma^2$ (2.9)
$\gamma = \sqrt {a^2\hat{n_x}^2 + b^2\hat{n_y}^2 + c^2\hat{n_z}^2}$

• 정규화 상수 $\gamma$를 구하는 식

 
또한

$\overrightarrow{h} = h\hat{n_s}$

$\overrightarrow{h}$ 는 타원체 표면에서 법선 방향으로의 변위 벡터
즉, $\overrightarrow{h}$ 는 타원체 표면의 한점에서 법선 벡터 방향으로의 거리 $h$ 만큼 떨어진 점의 위치 변화$h$ 는 타원체 표면에서 해당 점까지의 거리

 

$∵$ $r$ = $r_s$ + $h\hat{n_s}$ (2.10)

• 최종적으로, 타원체 표면 $r_s$으로부터 높이 $h$만큼 떨어진 점의 위치를 결정하는 식

---

 

WGS84 → Geographic coordinates

일반적으로 WGS84에서 지리적 좌표로 변환하는 것은 반대 방향으로 변환하는 것 보다 더 많은 작업이 필요하므로 여러 단계로 나눈다.

$\hat{n_s} = \frac{n_s}{||n_s||}$ (2.4 참고)
$\lambda = \arctan \frac{\hat{n_y}}{\hat{n_x}}$,
$\phi = arcsin \frac{\hat{n_z}}{||n_s||}$

 

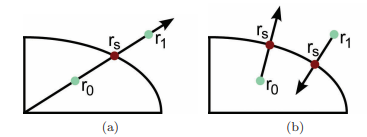
두 점 r0, r1을 Geocetnric, Geodetic 두 방식으로 나눠 크기를 조정할 수 있다.
 
(a) : Geocentric Nomrmal을 따라 타원체 중심의 벡터가 타원체와 교차하여 표면지점을 결정
(b) : Geocentric Nomrmal을 따라 반복 작업(뉴턴-랩슨법 사용)을 통해 스케일링

뉴턴-랩슨법 특징
1. 점진적으로 정답을 찾아가는 근사 해법이라서 빠르게 수렴함.
2. 삼각함수 없이 계산 가능 ⇒ 효율적이다.

 
 
Geocentric Nomrmal (a) 특징

• 계산이 간단함 (직선 방정식과 타원 방정식으로 해결 가능)
• 벡터 연산만 사용하므로 빠르게 계산 가능
• WGS84에서 지리 좌표계로 변환 했을 때 의 정확도를 보장할 수 없다.
  • 지구는 완벽한 구가 아니라 타원체 이기 때문.
• 따라서, Geocentric Nomrmal이 아닌 Geodetic Normal(b)을 사용해야 한다.

 
Geodetic Normal (b) 특징

• 정확도가 높음 (지구 타원체의 실제 표면을 고려함)
• WGS84 좌표 변환에서 가장 많이 사용됨
• 반복 연산이 필요함 (하지만 뉴턴 랩슨법을 통해 빠르게 수렴함)

$\overrightarrow{r} = r - \overrightarrow{0}$
$r = (x, y, z)$ 지구 중심에서의 위치를 의미
$\overrightarrow{r_s} = \beta \overrightarrow{r}$
$\beta$ = 크기 조정(scaling) 계수로, $\overrightarrow{r}$을 조정하여 표면에 맞춤
$\beta = \frac{1}{\sqrt{\frac{x^2}{a^2} + \frac{y^2}{b^2} + \frac{z^2}{c^2}}}$ (2.11)

• $\overrightarrow{r_s}$ 의미
  • 주어진 점 $(x,y,z)$이 지구 중심에서 어디에 있든, 이 점을 타원체 표면으로 옮겨야 함
  • 즉, $(x,y,z)$ 를 적절한 비율로 축소(Scaling)하여 $(x_s,y_s,z_s)$를 만들고 싶음
  • 이때, 스케일링 계수를 β 로 두고 아래처럼 표현
    $x_s = \beta x$
    $y_s = \beta y$ (2.12)
    $z_s = \beta z$
  • 즉, β값을 곱해서 현재 점을 표면으로 투영하는 방식
• $\beta$ 의 역할
  • 현재 점을 지구 중심 방향으로 투영하여, 타원체 표면 위로 스케일링하는 역할
  • 만약 주어진 점이 지구 표면과 가깝다면, $\beta≈1$에 가까워짐
  • 만약 주어진 점이 지구 표면보다 훨씬 멀다면, $β$가 작아져서 점을 더 많이 축소함
• $\beta$ 값 유도 과정 (2.11)
  • $(x_s, y_s,z_s)$는 타원체 표면에 있으므로 타원체 방정식을 만족해야한다.$\beta^2$ 값에 대해 정리하면 정리하면$\beta$ 값은 양수여야 하므로
  • $\beta = \frac{1}{\sqrt{\frac{x^2}{a^2} + \frac{y^2}{b^2} + \frac{z^2}{c^2}}}$ (2.11)
  • → $\beta^2(\frac{x^2}{a^2} + \frac{y^2}{b^2} + \frac{z^2}{c^2}) = 1$
  • → $\frac{(\beta x)^2}{a^2} + \frac{(\beta y)^2}{b^2} + \frac{(\beta z)^2}{c^2} = 1$

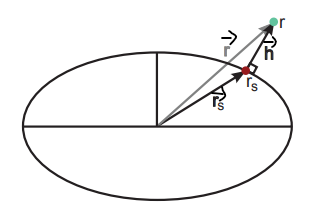
$\overrightarrow{r} = \overrightarrow{r_s} + \overrightarrow{h}$ (2.13)
$\overrightarrow{r}:$ 임의의 점 벡터 (구하고자 하는 점 위치)
$r_s:$ 표면에 있는 점 벡터
$\overrightarrow{h}:$ 표면 점으로부터 임의의 점 높이 벡터

• $\overrightarrow{h}$는 $\overrightarrow{n_s}$ 와 같은 방향을 가지지만 크기(magnitude)가 다르다.
  ⇒ $\overrightarrow{h} = \alpha \overrightarrow{n_s}$
  $\overrightarrow{n_s}:$ 지구 중심에서 표면점에 대해 정규화되지 않은 벡터
• $\overrightarrow{n_s} = \frac{x_s}{a^2}\hat{i} + \frac{y_s}{b^2}\hat{j} + \frac{z_s}{c^2}\hat{k}$ (2.14)

이 식을 (2.13)에 대입하면
$\overrightarrow{r} = \overrightarrow{r_s} + \alpha \overrightarrow{n_s}$
$\overrightarrow{r}$을 $\overrightarrow{r_s}$와 $\alpha \overrightarrow{n_s}$를 이용해서, 세 개의 스칼라 방정식( $x, y, z)$ 으로 나타내면

$x = x_s + \alpha \frac{x_s}{a^2},$
$y= y_s + \alpha \frac{y_s}{b^2},$
$z= z_s + \alpha \frac{z_s}{c^2}$

 
이 식을 인수 분해 하면

$x = x_s(1 + \frac{\alpha}{a^2}),$
$y = y_s(1 + \frac{\alpha}{b^2}),$
$z = z_s(1 + \frac{\alpha}{c^2})$

 
이 식을 표면에 있는 점을 기준으로 재배열 하면

$x_s = \frac{x}{1 + \frac{\alpha}{a^2}},$
$y_s = \frac{y}{1 + \frac{\alpha}{b^2}},$ (2.15)
$z_s = \frac{z}{1 + \frac{\alpha}{c^2}}$

즉, 알고 있는 점 $r = (x, y, z)$와 타원체의 반지름 $(a, b,c)$을 통해 $(x_s, y_s, z_s)$를 나타냈다.
식 (2.15) 에서 모르는 미지수는 $\alpha$ 이다.
 
즉, 미지수 $\alpha$만 찾으면 WGS84 좌표에서 임의의 점 $r$에 대해Geographic 좌표로 변환된 $\overrightarrow{r}$을 찾을 수 있다.
미지수 $\alpha$를 찾기 위해 타원체 방정식$(S)$ 에 $(x_s, y_s, z_s)$를 대입한다. (2.17)
 

$S = \frac{x_s^2}{a^2} + \frac{y_s^2}{b^2} + \frac{z_s^2}{c^2} - 1 =0$ (2.16)

 

$S = \frac{x^2}{a^2(1 + \frac{\alpha}{a^2})^2} + \frac{y^2}{b^2(1 + \frac{\alpha}{b^2})^2} + \frac{z^2}{c^2(1 + \frac{\alpha}{c^2})^2} - 1 =0$ (2.17)

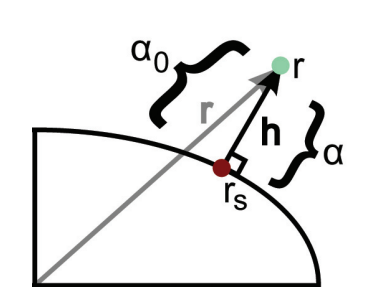
$\alpha_0 = (1- \beta) \frac{||r||}{||n_s||}$

• $(1-\beta)$ 의미
  • $\beta$ 값은 (2.11 참고)
  • 현재 점이 표면에서 얼마나 떨어져 있는지를 나타내는 비율
  • $\beta$가 크면 현재 점이 표면에 가까워짐
  • $\beta$가 작으면 현재 점이 표면에서 멀리 떨어져짐
• $\frac{||r||}{||n_s||}$ 의미
  • 현재 좌표에서 법선 방향으로 얼마나 이동해야 하는지를 계산하는 기준
  • $||r|| :$중심으로부터 임의의 점 $(x, y,z)$벡터 $\overrightarrow{r}$ 크기
    • 원래 주어진 WGS84 좌표의 벡터 크기
  • $||n_s||:$중심으로부터 지구 표면에 있는 점 $(x_s, y_s,z_s)$벡터 $\overrightarrow{n_s}$크기
    • 표면 좌표에서의 법선 벡터 크기
• 뉴턴 랩슨법
  • 초기 값 : $\alpha_0$
  • $\alpha_{n+1} = \alpha_n - \frac{S(\alpha_n)}{S^\prime(\alpha_n)}$해당 작업을 통해 $\alpha$를 찾고, (2.17)에 대입하여 0과 근사해지는 값을 찾음.
    • 코드 예시
      • $\alpha$를 대입해 S 값이 0과 가까운 $10^{-10}$보다 작은 경우까지 반복
        
  • ⇒ $\alpha =\alpha - \frac{S}{\frac{{\partial S}}{\partial \alpha}}$
  • $\frac {\partial S}{\partial \alpha} = -2[\frac{x^2}{a^4(1+\frac{\alpha}{a^2})^3} + \frac{y^2}{b^4(1+\frac{\alpha}{b^2})^3} + \frac{z^2}{c^4(1+\frac{\alpha}{c^2})^3}]$
• 타원체 방정식$(S)$과 뉴턴-랩슨법을 이용
• $S$ 와 $\frac {\partial S}{\partial \alpha}$를 평가하여 0에 가까워지는 $\alpha$를 찾는다.
• 즉 미지수 $\alpha$를 근사해, 현재 위치와 타원체 표면 사이의 거리를 근사적으로 계산한다.